Indefinite Integration of the Gamma Integral
and Related Statistical Applications
4.3 Exponential Integral Function
The exponential integral is seldom referred to as a distribution (Meijer & Baken, 1987
). However, it is a function crucial in physics and engineering science, particularly in thermal engineering (Biegen & Czanderna, 1972), hydrogeology (Barry et al., 2000), stellar
atmosphere (Mihalas, 2006), and petroleum engineering (Donnez, 2007).
The simplest version of the exponential integral is defined as
\begin{equation*}
{{E}_{(1)}}\left( x \right)=\int_{1}^{\infty }{\frac{{\exp(-xt)}}{t}dt}.
\end{equation*}
It can be transformed into a general form of the gamma integral
\begin{align*}
{{E}_{(1)}}\left( x \right) &=\int_{x}^{\infty }{{{t}^{-1}}{\exp(-t)}dt} \\ \notag
& ={\exp(-c)}h_{-1}^{-c}{\Bigr|}_{c\to \infty}-{\exp(-x)}h_{-1}^{-x}. \tag{4.1}
\end{align*}
[Proof for 4.1)]
Similarly, the $n$th-order exponential integral can be expressed as an upper incomplete gamma function, where the base parameter belongs to negative integers
\begin{align*}
{{E}_{(n)}}\left( x \right) &={{x}^{n-1}}\int_{x}^{\infty }{{{t}^{-n}}{\exp(-t)}dt} \\ \notag
& ={{\left( \frac{x}{c} \right)}^{n-1}}{\exp(-c)}h_{-n}^{-c}{\Bigr|}_{c\to \infty}-{\exp(-x)}h_{-n}^{-x}. \tag{4.2}
\end{align*}
[Proof for 4.2)]
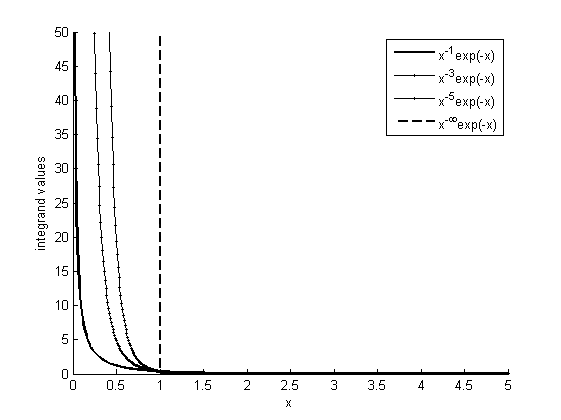
Figure 6: Functional Plots of $x^{-n}\exp(-x)$
We need to estimate two sources of error when applying the "$h$" factorization method. The
first is associated with the power parameter $c$. As Figure 6 shows, given a considerably larger number $C$,
${{E}_{(1)}}$ has the largest error of all ${{E}_{(n)}}$. The upper limit of the error can thus be evaluated with the integral
\begin{equation}
\int_{C}^{\infty }{{{t}^{-1}}{\exp(-t)}dt}. \tag{4.3}
\end{equation}
[Proof for 4.3)]
The result indicates that the errors are $4.16e-06$, $9.84e-11$, $8.05e-15$ for $C=10$, $20$, and $30$, respectively, if we use $10^{6}$ as the operational definition of infinity.
In addition to the error that results from $C$, we need to consider another source of error that is associated with the
"$h$" function when the base argument $s$ is a negative integer. As (3.1)
illustrates, all of $h_{s,s\in {{\mathbb{Z}}^{-}}}^{c}$ can be reduced to a function of $h_{-1}^{c}$, which requires summing an infinite
number of $h_{s,s\in {{\mathbb{Z}}^{+}_{0}}}^{-c}$. For any given $-c$, $h_{s,s\in {{\mathbb{Z}}^{+}_{0}}}^{-c}$ will slowly converge to
zero if $s\to \infty $. Therefore, for computational purposes, we must determine a definitive number of the terms $t$ to calculate this
infinite series, and this decision is bound to generate a certain level of error. Notice that the exponential integrals after
transformation can all be respecified as an improper integral. To evaluate this source of error, we can calculate the sum of the omitted
terms under a given value $C$. Since ${{E}_{(1)}}$ has the heaviest tail, we use it to evaluate the upper limit of this error by
\begin{equation*}
{{E}_{\left( 1 \right)}}\left( x;C,t \right)-{{E}_{\left( 1 \right)}}\left( x;C \right)=\underset{n\to \infty }
{\mathop{\lim }}\,\,\,\sum\limits_{s=t+1}^{n}{\left( h_{s}^{x}-h_{s}^{C} \right)}, \tag{4.4}
\end{equation*}
where $t$ represents the number of summation terms.
[Proof for 4.4)]
If we set $x=0.5$, $C=10$ and use $10^{6}$ as the operational definition of infinity, the errors for $t=10^{2}$, $10^{3}$, $10^{4}$, $10^{5}$ are $8.87e-02$, $9.42e-03$, $9.40e-04$, and $8.64e-05$, respectively. This indicates the level of precision is $m-1$ decimal places for using $10^{m}$ terms to compute $h_{-1}^{-C}$. Comparing this result with the first error related to $C$, we conclude that the second source of error is more restrictive, since we need $t=10^{6}$ terms in summing the series to reach 5 significant digits, equivalent to the maximal level of precision predicted by (4.3) for $C=10$ without any restriction on $t$.
The above discussion reflects that the speed of convergence is a dominant factor that limits the overall level of precision. As (4.5) shows, the computation of ${{E}_{\left( 1 \right)}}\left( x;C,t \right)$ is composed of a baseline estimate $\log \left| C/x \right|$ and $t$ negative subtracting terms $\sum\limits_{s=0}^{t}{\left( h_{s}^{C}-h_{s}^{x} \right)}$, since $h_{s}^{C}<h_{s}^{x}$ for $C>0$ and $x>0$. While a larger $C$ can increase precision level by reducing the first source of error, doing so biases the baseline estimate upward, and thus requires more items to achieve convergence
\begin{equation*}
{{E}_{\left(1\right)}}\left(x;C,t\right)=\log\left|\frac{C}{x} \right|+\sum\limits_{s=0}^{t}{\left( h_{s}^{C}-h_{s}^{x} \right)}.
\tag{4.5}
\end{equation*}
[Proof for (4.5)]
For instance, if we use the upper limit $C$ and $t$ summation terms to compute ${{E}_{(1)}}\left( x \right)$, the error
$k_{1}$ can be specified as
\begin{align*}
{{k}_{1}}&={{E}_{\left( 1 \right)}}\left( x;C,t \right)-{{E}_{\left( 1 \right)}}\left( x \right) \\
& =\log(C)-\log(x)+\sum\limits_{s=0}^{{{t}}}{\left( h_{s}^{C}-h_{s}^{x} \right)}-{{E}_{\left( 1 \right)}}\left( x \right). \notag
\end{align*}
Provided that we increase the upper limit to $\lambda C$ $\left( \lambda >1 \right)$, the new error $k_{2}$ with $t$ summation terms will be larger than $k_{1}$
\begin{align}
{{k}_{2}}>&{{k}_{1}}+\left( \lambda -1 \right){\exp(-C\lambda )}\left[ 1+\left( \lambda -1 \right)\left( C-1 \right)h_{1}^{-C\left(
\lambda -1 \right)} \right] \notag \\
& +\sum\limits_{i=0}^{\infty }{{{\left[ C\left( \lambda -1 \right) \right]}^{i+1}}{\exp(-C\left( \lambda -1
\right))}h_{t+1+i}^{C}h_{i}^{-C\left( \lambda -1 \right)}}, \tag{4.6}
\end{align}
where all the three terms in the RHS equation are positive.
[Proof for 4.6)]
This means that, despite the fact that increasing $C$ can improve computational precision, the cost is slower convergence. With a given computational capacity, a tradeoff has to be made between the two sources of error for computing ${{E}_{(n)}}\left( x \right)$ efficiently. To evaluate this problem, we carry out a simulation study to see how the two sources of error interact under different settings of $C$ and $t$. The precision level is set $C=5,10,15,20$, and the target of analysis includes three definite exponential integrals ${{E}_{\left( 1 \right)}}\left( x \right)$, ${{E}_{\left( 5 \right)}}\left( x \right)$, and ${{E}_{\left( 10 \right)}}\left( x \right)$, in which the lower limit $x$ is set $0.5$. For each definite integral, we compute the result by changing the number of summation terms from ${{10}^{3}}$, ${{10}^{4}}$, ${{10}^{5}}$ to ${{10}^{6}}$. The overall analysis contains $48$ trials of numerical computations.
The simulation result in Table 2 confirms that the number of summation terms $t$ plays a dominant role in determining the precision level of numerical computation, especially in lower-order cases. For instance, when evaluating ${{E}_{(1)}}\left( 0.5 \right)$ with varying upper limits $C$, we found that $C=5$ and $C=10$ has the best precision estimate under $t=10^{3}, 10^{4}$ and $t=10^{5}, 10^{6}$, respectively. The actual precision level fits the rule of $m-1$ digits with $10^{m}$ summation terms very well. For higher-order cases, the precision level improves very quickly and only $10^{3}$ terms are needed to achieve 4 and 10 significant digits under $C=5$ for ${{E}_{(5)}}\left( 0.5 \right)$ and ${{E}_{(10)}}\left( 0.5 \right)$. The overall result indicates that a considerably larger $C$ can be as moderate as $5$ or $10$, and the level of numerical precision is largely determined by the number of summation items $t$.
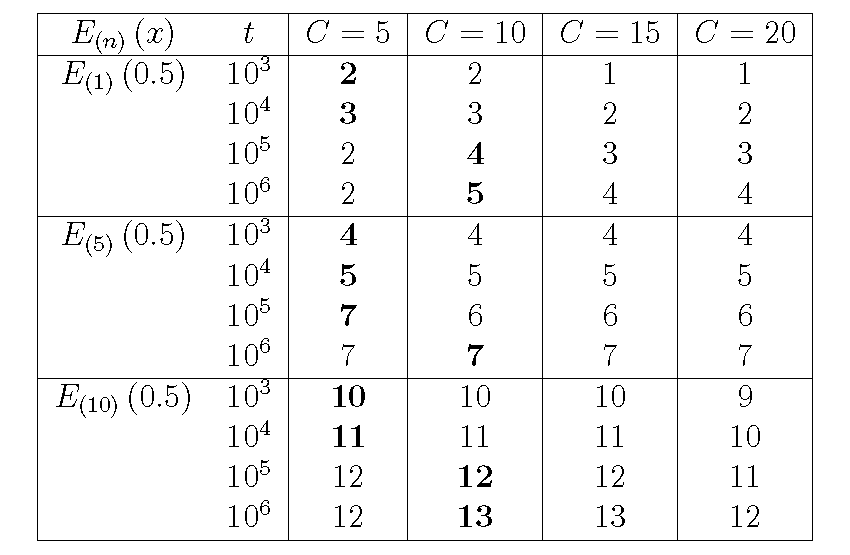
Table 2: Simulation Results of Numerical Precision by Varying C and t
