Logo

3.2 Parameter Constraints

The model specification in Section 3.1 is deduced from a regression model that fixes all the variables at the minimum level with the exception of the constant covariate. After being fixed, the covariate matrix is expressed with an asterisk sign ${{x}^{*}}$. The predicted value of the dependent variable is bounded within the lower and upper limits, $a$ and $b$. The eligible parameter space of the beta coefficient ${{\beta }_{m}}$ can be derived by (1) fixing the independent variables of interest at the minimum, while finding the greatest and least predicted values, $\hat{y}_{\sim m}^{\max }$ and $\hat{y}_{\sim m}^{\min }$, (2) varying the covariate value of interest from minimum to maximum to derive its largest or least possible contribution, $b$ and $a$, and (3) dividing the largest and least possible contribution by the maximum range $x_{1}^{*\max}-x_{1}^{*\min}$, where $x_{1}^{*\min}=0$.13 Figure 1 illustrates this procedure as the above describes.

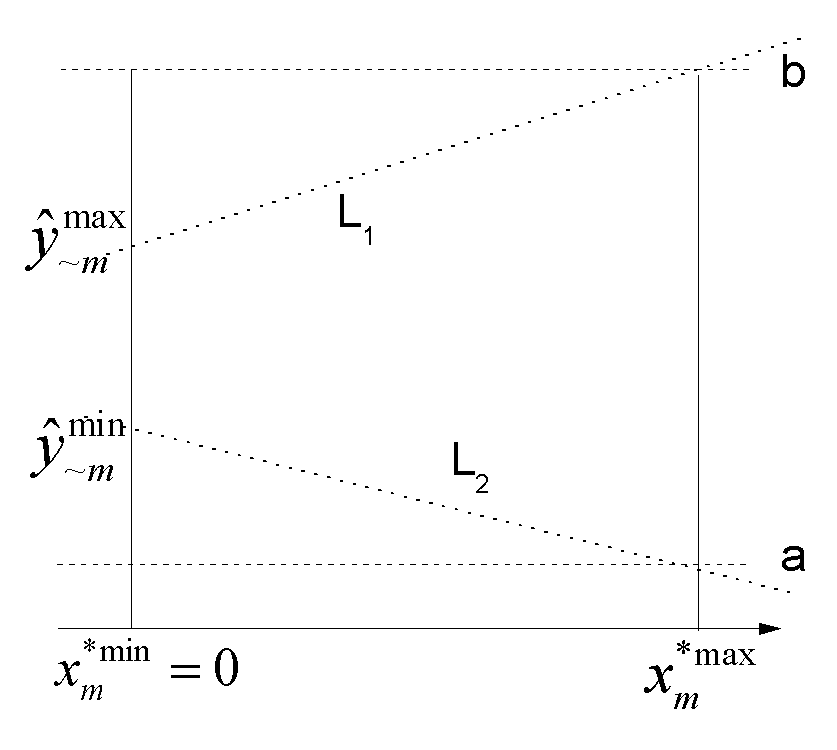
Figure 1

Figure 1 Boundary Constraints of $\beta_{m}$

The first two constraints define the upper and lower bounds of the predicted value for the dependent variable. The third and four constraints specify the range of the constant, which refers to the level of the dependent variable when all the covariates are held at the minimum; and apparently, the upper and lower limits are the same as the dependent variable. For the rest of $2m$ equations, constraints are about the admissible parameter space of beta coefficients from ${{x}_{1}}$ to ${{x}_{m}}$. The two additional constraints specify the maximum and minimum value of the scale parameter. The maximum is set to the full range because the distribution will deviate from truncated normal and approach uniform distribution when $\sigma \gg \left| b-a \right|$. The minimum is set to an arbitrary small number $\kappa$ to prevent negative variance from occurring.

____________________

Footnote

13 If the interaction terms are fixed at the minimum at the same time as other variables, we will not be able to derive $x_{1}^{*}\times x_{2}^{*}={{\left( {{x}_{1}}\times {{x}_{2}} \right)}^{*}}$, as the previous discussion about (2.3) and (2.4) explains.

Download [full paper] [supplementary material A] [supplementary material B] [all replication files]