Solving the Unsolvables

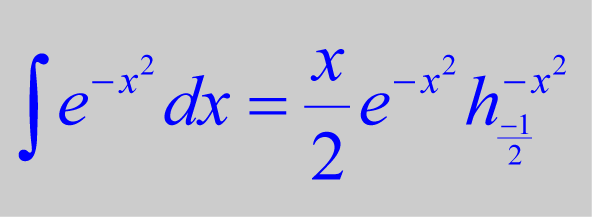
Liouville's theorem proves that certain integrals cannot be evaluated with elementary functions. It demonstrates why the gamma, exponential and Gaussian integrals lack antiderivatives. However, by applying the "h" factorization method, I present an analytical solution to the antiderivative of the gamma integral. This solution applies to all integrals that can be transformed into a gamma integral, such as the Gaussian integral.

Fixing Boundary Violations

Much political science research involves analysis of a trunacted dependent variable. These studies are likely to generate out-of-bounds predicted values. I find that both the OLS and truncated regression models suffer from boundary violations, and hence, I propose a revised truncated regression model with constrained optimization and successfully eliminates boundary violations.

Improving panel regression

Political science studies commonly analyze panel data of truncated dependent variables. Unfortunately, panel regression for this data type contains three methodological problems: boundary violations, parameter estimation, and model specification. I explain the nature of these problems and propose three models to solve boundary violations by applying constrained optimization in the least squares and maximum likelihood paradigms.

Download

Related Works

How to Cite

Copyright Policy